
Balancing Complexity and Accuracy: Variable Selection in Lasso
In Lasso regression, a new predictor (regressor) is included in the model only if the improvement in predictive accuracy (marginal benefit) outweighs the increase in model complexity (marginal cost) due to adding the predictor. This helps prevent overfitting by ensuring that only predictors that contribute significantly to the model’s performance are included.
Mathematical Explanation
Let’s consider a linear regression model:

In Lasso regression, we solve the following optimization problem:
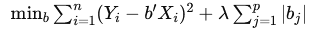
where:
- The first term is the sum of squared errors.
- The second term is the penalty term, proportional to the sum of the absolute values of the coefficients bj.
- λ is the penalty parameter controlling the strength of regularization.
Marginal Cost: The penalty term λ∑∣bj∣ introduces a cost for each non-zero coefficient bj. This cost increases with the number of non-zero coefficients, discouraging the inclusion of predictors that do not significantly improve the model’s predictive accuracy.
Marginal Benefit: The benefit of adding a predictor Xj is the improvement in the model’s predictive accuracy, measured by the reduction in the sum of squared errors.
Practical Importance
- Preventing Overfitting: By ensuring that only predictors with significant marginal benefits are included, Lasso prevents the model from becoming overly complex and fitting to noise in the data. This leads to better generalization to new, unseen data.
- Simplicity and Interpretability: A model with fewer predictors is easier to interpret and understand. By including only the most important predictors, Lasso creates a simpler and more interpretable model.
- Efficiency: Reducing the number of predictors included in the model makes computation more efficient, which is especially important in high-dimensional settings with many predictors.
Example
Consider a model predicting student performance based on various features such as hours studied, attendance, participation, and many other less relevant factors. Let’s denote these predictors as X1, X2,…, Xp
- Marginal Benefit: Adding a predictor like “hours studied” (X1) may significantly improve the model’s accuracy because it has a strong relationship with student performance. The reduction in the sum of squared errors when including X1 is high.
- Marginal Cost: Adding a predictor like “color of the notebook” (Xp) introduces a cost λ∣bp∣. If the predictor has a very small coefficient (little to no effect on the outcome), the cost of including it (penalty term) outweighs the benefit (reduction in the sum of squared errors).
Mathematical Illustration:
- Assume λ=0.1 and the coefficient for “hours studied” is estimated as b1=0.5. The marginal cost of including X1 is 0.1 × 0.5=0.05, while the marginal benefit is high.
- For “color of the notebook,” suppose the coefficient is bp=0.01 The marginal cost is 0.1 × 0.01=0.001, but the marginal benefit is negligible, making the overall gain negative when considering the penalty.
Therefore, the Lasso regression will likely include “hours studied” in the model but exclude “color of the notebook.”
Summary
The principle that the marginal cost of adding a regressor must be less than the marginal benefit is fundamental to Lasso regression. It ensures that only predictors that contribute significantly to improving the model’s accuracy are included, preventing overfitting and creating a simpler, more interpretable model. This balance between fit and complexity is achieved through the penalty term, which discourages the inclusion of predictors with small coefficients that do not substantially improve the model’s performance.
