Ahmed Dawoud

Approximate sparsity refers to the situation in a high-dimensional regression model where only a small number of predictors (regressors) have significant (large) coefficients, while the majority of predictors have coefficients that are either zero or very close to zero. This concept is crucial in high-dimensional settings, where the number of predictors pp is large, often much larger than the number of observations n.

Mathematical Explanation

Let’s consider a linear regression model:

In high-dimensional settings, pp can be much larger than n. Classical least squares regression fails in this context because it tends to overfit the data, leading to poor out-of-sample predictions.

Approximate sparsity assumes that most of the coefficients βj​ are zero or very close to zero. This can be mathematically expressed as:

Example: Suppose p=1000 (i.e., 1000 predictors) and we observe that only the first 10 predictors have significant coefficients, while the rest are close to zero. The coefficients might look like this: β1=0.5,  β2=0.3,  β3=0.2,  …,  β10=0.05,  β11≈0,  …,  β1000≈

Practical Importance

1. Improved Model Interpretability:
   • Approximate sparsity helps in identifying the most important predictors, making the model easier to interpret. For instance, in predicting house prices, knowing that only a few factors like location, square footage, and number of bedrooms are important simplifies understanding and communicating the model.
2. Enhanced Predictive Performance:
   • By focusing on the significant predictors and ignoring the irrelevant ones, models adhering to approximate sparsity avoid overfitting and often perform better on new, unseen data. This leads to more reliable predictions.
3. Efficient Computation:
   • High-dimensional datasets can be computationally expensive to handle. Approximate sparsity reduces the number of predictors considered, making the computation more efficient. For example, if only 10 out of 1000 predictors are important, we only need to focus computational resources on these 10.

Practical Example with Clear Math

Let’s take a practical example of predicting house prices. Suppose we have the following data:

• p=1000 (predictors like square footage, number of bedrooms, age of the house, distance to the nearest school, etc.).
• n=100(observations)

Assume the true model is:

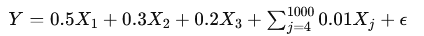
Here, only the first three predictors have significant coefficients, and the rest have very small coefficients (0.01).

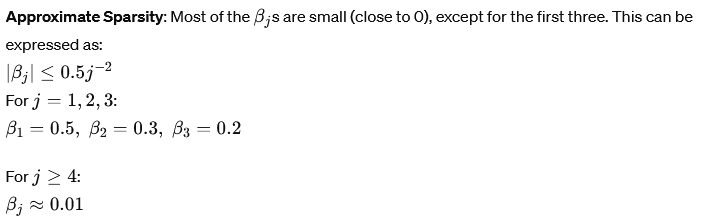
Why It Matters:

• If we use a regular linear regression, the model might overfit by trying to use all 1000 predictors.
• Using Lasso regression, which enforces sparsity, the model will shrink the coefficients of the less important predictors (from X4​ to X1000​) towards zero and retain only the significant ones (X1,X2,X3​).

Lasso Regression Example:

Lasso solves:

Summary

Approximate sparsity is a crucial concept in high-dimensional regression, ensuring that only the most important predictors are considered. This leads to models that are interpretable, computationally efficient, and have better predictive performance on new data. By leveraging techniques like Lasso regression, we can effectively handle high-dimensional data and avoid the pitfalls of classical regression methods.