Category Archives: Data Analysis

Cracking the Code: A Guide to Bambi’s Hierarchical Formula Syntax
I am learning Bayesian inference, currently working my way through the fantastic “Statistical Rethinking” book and implementing the code examples in PyMC. For someone who has spent years using the frequentist approach, thinking in probabilities is a real but rewarding challenge. To ease this transition, I decided to start with Bambi, a library that makes…
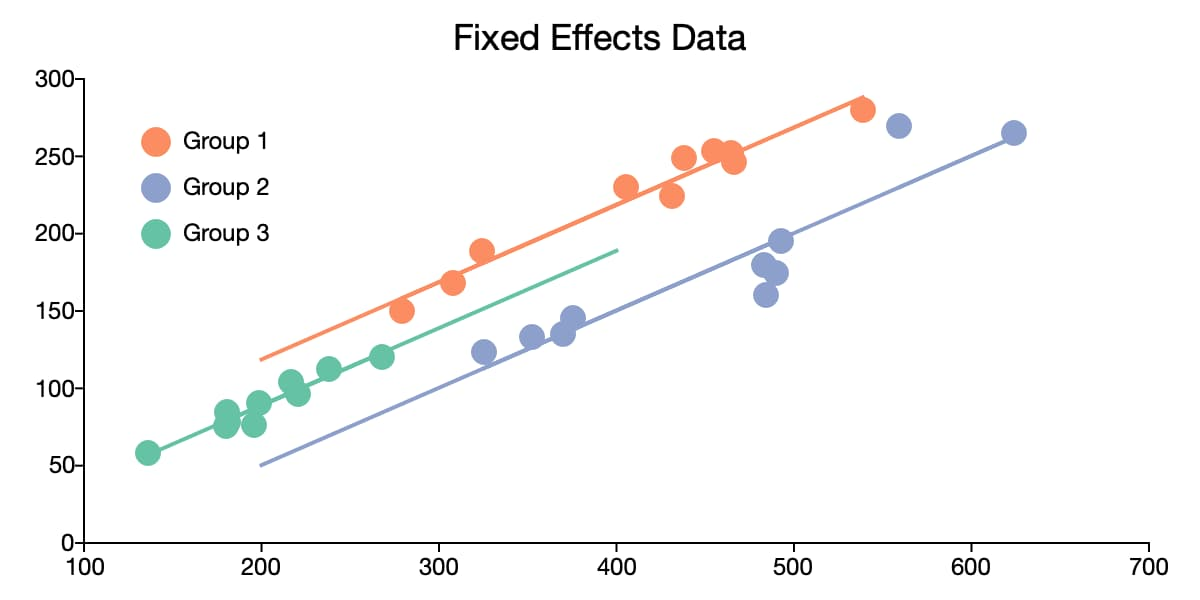
Unlocking the Power of Panel Data: A Beginner’s Guide with Python’s linearmodels
If you’re delving into data analysis, you’ve likely encountered cross-sectional data (data at one point in time) or time-series data (data over time for one entity). But what if you have data on multiple entities observed over multiple time periods? Welcome to the world of panel data! Panel data is incredibly powerful because it allows…

Mastering Pandas: A Comprehensive Step-by-Step Guide to Efficient Data Analysis
In this blog post, I share all the Pandas materials that I have written over the past couple of months in an organized, easy-to-follow, logical, step-by-step tutorial. Whether you’re a beginner looking to get started or an experienced user aiming to deepen your understanding, this comprehensive guide will provide you with the essential functions and…
Causal ML Book: Summary of Key Concepts from Chapter 5
Causal inference is a cornerstone of research and analysis in many fields, from economics to medicine to social sciences. Chapter 5 of the Causal ML Book delves into advanced methodologies that ensure comparability between treatment and control groups, which is crucial for valid causal inference. This post will summarize the key concepts discussed in Chapter…

Understanding Neyman Orthogonality in High-Dimensional Linear Regression
Introduction In the realm of data science and statistics, accurately determining the relationships between variables is essential, particularly when dealing with high-dimensional data. High-dimensional settings, where the number of predictors (p) is large relative to the number of observations (n), pose significant challenges for traditional statistical methods. This blog post delves into the concept of…

Penalized Regression Methods: Lasso, Ridge, Elastic Net, and Lava Explained
In the realm of high-dimensional data analysis, traditional linear regression techniques often fall short due to the presence of numerous predictors, which can lead to overfitting and poor predictive performance. To address these challenges, penalized regression methods introduce penalties to the regression model, effectively shrinking the coefficients and providing a balance between model complexity and…

Balancing Complexity and Accuracy: Variable Selection in Lasso
In Lasso regression, a new predictor (regressor) is included in the model only if the improvement in predictive accuracy (marginal benefit) outweighs the increase in model complexity (marginal cost) due to adding the predictor. This helps prevent overfitting by ensuring that only predictors that contribute significantly to the model’s performance are included. Mathematical Explanation Let’s…

Why Lasso Does Not Guarantee Correct Variable Selection? A Thorough Explanation
While Lasso regression helps in variable selection by shrinking some coefficients to zero, it does not guarantee that it will select the exact set of true predictors. This limitation is especially pronounced in situations where predictors are highly correlated or when the true model does not exhibit strong sparsity. Mathematical Explanation Let’s consider the linear…
