
Detailed Explanation of Partialling-Out and the Frisch-Waugh-Lovell (FWL) Theorem
Partialling-Out
Partialling-out is a technique used in regression analysis to isolate the effect of a specific variable (regressor) on the outcome by removing the influence of other variables (control variables). This helps us understand the true relationship between the target regressor and the outcome.







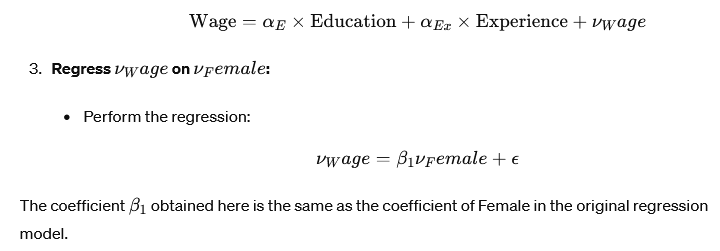

Summary
- Partialling-out: A process to isolate the effect of one variable by removing the influence of other variables. It involves regressing both the target variable and the outcome on the control variables and using the residuals in a subsequent regression.
- FWL Theorem: A formal theorem proving that the coefficient of a variable obtained from partialling-out is the same as the coefficient from the original regression model. It validates the partialling-out process and simplifies regression analysis by breaking it into manageable steps.
