Ahmed Dawoud

---

In the world of data science and machine learning, linear regression stands as a foundational tool for predictive modeling. Despite its simplicity, its proper implementation, especially in high-dimensional settings, demands a nuanced understanding. This blog post dives into the intricacies of linear regression, focusing on how dimensionality impacts wage gap estimates and the challenges associated with estimating standard errors in such contexts.

Foundation of Linear Regression

Linear regression aims to predict an outcome variable Y using a set of predictor variables X. The goal is to construct the best linear prediction rule, which can be written as:

Here, β represents the regression coefficients that minimize the mean squared error (MSE) between the predicted and actual values of Y.

The Best Linear Prediction Problem

In practice, researchers do not have access to the entire population data but work with samples. When working with samples, the objective is to find the best in-sample linear prediction rule. This involves replacing theoretical expected values with empirical averages. The resulting coefficients, β^​, are known as Ordinary Least Squares (OLS) estimates. These estimates are derived by minimizing the sample MSE:

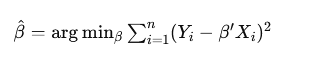
Proper Estimation of Standard Errors

A critical aspect of regression analysis is the estimation of standard errors, which measure the variability or uncertainty around the coefficient estimates. Traditional methods like the Eicker-Huber-White standard error (HC0) and the jackknife standard error (HC3) have varying performances in different contexts. In high-dimensional settings, where the number of predictors (p) is large relative to the number of observations (n), these methods can behave differently.

• HC0 (Eicker-Huber-White): Known to be inconsistent and often too small in high-dimensional settings.
• HC3 (Jackknife): More reliable than HC0 but still has limitations.

Dimensionality and Its Impact on Wage Gap Estimates

An important application of linear regression is in estimating wage gaps between different groups. Consider a log-linear regression model to estimate the wage gap between male and female workers:

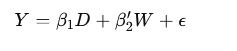
Here, Y is the log-wage, D is an indicator variable for being female, and W includes other wage determinants like education, experience, region, occupation, and industry indicators. The interaction terms between these variables also play a crucial role in capturing the complexity of wage determination.

Empirical Findings

When analyzing wage gaps using different regression methods, several key observations emerge:

• Unconditional Wage Gap: The simple difference in log-wages between male and female workers in our sample, which is about 3.8% in favor of male workers.
• Conditional Wage Gap: After controlling for various job-relevant characteristics, the wage gap increases to about 7%, indicating that female workers earn approximately 7% less than their male counterparts with similar characteristics.

Partialling-Out Approach

The partialling-out approach helps isolate the effect of the target variable (D) by removing the influence of control variables (W). This method provides a numerically identical estimate for the coefficient β1​, reaffirming the Frisch-Waugh-Lovell (FWL) theorem, which states that the coefficient on D in a regression that includes W is the same as the coefficient from regressing the residuals of Y and D after removing the influence of W.

Double Lasso Procedure

In high-dimensional settings, the Double Lasso procedure emerges as a robust alternative to traditional OLS. It handles a large number of predictors by performing variable selection, thus mitigating the risk of overfitting. The Double Lasso procedure remains consistent and provides reliable standard error estimates even when p≫n.

Practical Implications

The punchline is clear: in high-dimensional settings, OLS is no longer adaptive. This lack of adaptivity means that the conventional properties of OLS, like reliable standard errors, do not hold, making other procedures, such as Double Lasso, highly preferable. This insight is crucial for researchers and practitioners working with complex models and large datasets, ensuring more accurate and reliable inferences.

Conclusion

Linear regression, while straightforward in theory, presents significant challenges in high-dimensional settings. Proper estimation of standard errors, understanding the impact of dimensionality, and choosing the right methods like Double Lasso over traditional OLS can lead to more accurate and reliable results. As data science continues to evolve, these insights will help practitioners navigate the complexities of high-dimensional data and make informed decisions based on robust statistical analysis. To put it simply:

• OLS standard errors (both HC0 and HC3) are not reliable when p is close to n.
• Double Lasso standard errors remain stable and reliable, even in high-dimensional settings.